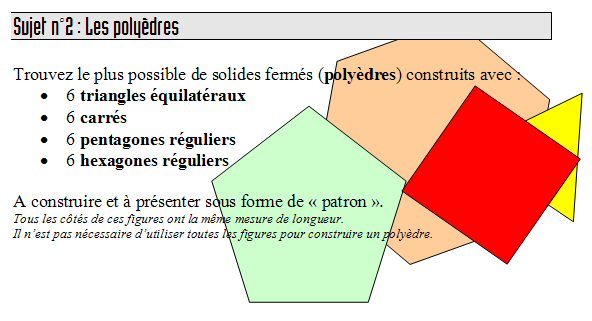
5 séries de problèmes, certains difficiles, avec 3 niveaux de difficultés différents proposés aux élèves de la Grande section à la Sixième.
- Léo et Léa ont ensemble 12 billes. Léa a 2 billes de plus que Léo.
Combien de billes a chaque enfant ?
- Une batte de base-ball et sa balle coûtent ensemble 11 €. La batte coûte 10 € de plus que la balle.
Quel est le prix de la balle ?
- On pèse des oranges, des bananes et des pommes.
Quand on pèse les bananes et les pommes, on mesure 8 kg. Quand on pèse les oranges et les pommes, on trouve 5 kg. Quand on pèse les les oranges et les bananes, 7kg.
Combien pèse chaque sorte de fruits ?
- Léa achète quatre jouets.
Tous les jouets, sauf le premier, coûtent ensemble 12,70 € . Si on n’achète pas le deuxième, cela coûte 8,80 €, ce sera 10,30 € si l’on exclut le troisième et enfin 13,20 € sans le quatrième.
Quels sont les prix des jouets ?
Aide : « Et si on achetait les 4 lots de jouets ? »
- Jules a 12 ans. Sa sœur, Sophie, a 7 ans de plus. Pierre la moitié de l’âge de Jules.
Quel âge a Sophie ? Quel âge a Pierre ?
- Julie a 21 ans. Sa sœur, Sophie, a le triple de l’âge de Pierre. Pierre a le tiers de l’âge de Julie.
Quel âge a Sophie ?
- Léo partage des bonbons avec 3 camarades : il garde la moitié du paquet pour lui et partage le reste équitablement.
Chaque enfant reçoit 6 bonbons.
Combien de bonbons contenait le paquet de Léo avant qu’il ne l’ouvre ?
- Léo ouvre son paquet de bonbons et partage d’abord équitablement 16 bonbons avec ses 3 amis.
Il laisse ensuite le paquet sur la table. A son retour, il remarque que d’autres bonbons ont été pris : il n’en reste que 7 dans le paquet, c’est pour lui ! Il interroge Léa : « Moi, j’ai juste pris un 1/3 de ce qu’il y avait. » Il interroge Pierre : « Après Léa, je n’en ai pris qu’un peu, j’en ai laissé 3/4. » Il interroge Jean : « C’est Pierre qui m’a dit d’en prendre le double de lui et effectivement il en restait 7. »
Combien de bonbons contenait le paquet de Léo avant qu’il ne l’ouvre ?
Combien de bonbons a eu chaque enfant ?
- Léo achète une trousse à 7 € et un classeur. Léa achète un classeur et une équerre. Elle paie 3 € de moins que Léo.
Combien coûte l’équerre ?
- Dans ce magasin, un classeur, un compas et une équerre, valent 7€ de moins qu’un classeur et 2 compas qui coûtent 24 €. Le compas coûte 3 € de plus que le classeur.
- Quel est le prix de chaque objet ?
Les fichiers :
1. Vous êtes mis au défi de trouver comment écrire les nombres de cette manière (en comptant jusqu’à 50 par exemple).
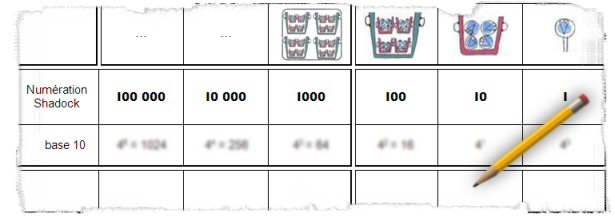
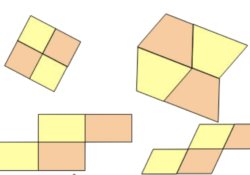
Plus rigoureusement, il s’agit sans tenir compte de l’ordre de déterminer les combinaisons possibles de 2 éléments parmi 10. (Le nombre de parties-coefficient binomial-de cardinal 2 dans un ensemble de cardinal 10).
